Simple covid19 logistic regression model

Content

• Italy covid19 logistic regression model
• Plots description
• General description
• The logistic model

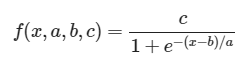
Still under construction!

For errors or criticism open an issue in the github repository kidpixo/COVID19-dashboard

Italy covid19 logistic regression model

• Dashboard
• Notebook

Latest Model Results 21/04/2020

NEW on 10 Apr I modified the model days window from 14 to 21 to have more stability in the model.

• a: 14.27± 0.43 : infection speed
• b: 93.60± 0.44 : the day with the maximum infections occurred 02/04/2020
• c: 238588.60± 3877.87 : the total number of recorded infected people at the infection’s end
• Day of 0 new infections 03/10/2020

Based on Covid-19 infection in Italy. Mathematical models and predictions

• Data from pcm-dpc/COVID-19: COVID-19 Italia - Monitoraggio situazione
• Dashboard COVID-19 ITALIA - Desktop

Plots description

• infection cumulative : cumulative number of infection.
• infection daily : daily number of infection.
• infection speed: the number of new infection cause by each person (paramter a in the model).
• max day : the day with the maximum infections occurred, this is the maximum of the daily curve (paramter b in the model).
• total infected : the total number of recorded infected people at the infection’s end (paramter c in the model).
• day of 0 infection : the day when the modeled daily infection drops to 0.

General description

I read the nice post Covid-19 infection in Italy. Mathematical models and predictions.

I want to do something useful and learn something, so I start reproducing the post.

The original post uses data from the Italian Civil Protection Department, that collects and pushes new data every day in their github repository CSSEGISandData/COVID-19.

I also start to use the global data from CSSEGISandData/COVID-19: Novel Coronavirus (COVID-19) Cases, provided by JHU CSSE, but this is not fully functional.

The main important point in the notebook are:

1. Get the data
2. Clean days with 'warnings' (missing data etc etc) : I delete the datapoint and interpolate, trusting the nearest points are good.
3. Define the logistic model (see below)
4. Start fitting the function on the latest 14 days, to take care of the evolving situation in each state.
5. Move the window from the beginning of the data to the end, producing a time series of the model paramter with error.
6. Generate new date to the point when there will be 0 daily infection, following the model.
7. Calculate predicted infection for each day in the future.
8. Propagate uncertainties.

The logistic model

(Text from Covid-19 infection in Italy. Mathematical models and predictions)

The logistic model has been widely used to describe the growth of a population. An infection can be described as the growth of the population of a pathogen agent, so a logistic model seems reasonable.

This formula is very known among data scientists because it’s used in the logistic regression classifier and as an activation function of neural networks.

The most generic expression of a logistic function is:

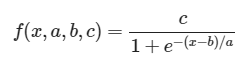
In this formula, we have the variable x that is the time and three parameters: a,b,c.

• a refers to the infection speed
• b is the day with the maximum infections occurred
• c is the total number of recorded infected people at the infection’s end

At high time values, the number of infected people gets closer and closer to c and that’s the point at which we can say that the infection has ended.

This function has also an inflection point at b, that is the point at which the first derivative starts to decrease (i.e. the peak after which the infection starts to become less aggressive and decreases).